DQN: Dueling Q-Network

Many deep RL algorithms use conventional deep neural networks such as the convolutional networks in DQN or LSTMs in DRQN. The dueling network takes a different approach. Instead of using the existing networks, a new neural network architecture was designed specifically for deep reinforcement learning.

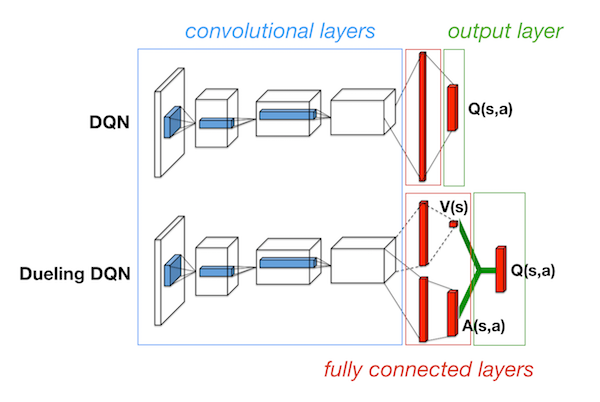
The dueling architecture enhances the original Q network in DQN. While keeping the same convolutional lower layers, it separates the upper fully connected layers into two streams: one predicts the state values $V$ and another predicts the advantage $A$ for each action in that state. Then, these two streams combine to produce a single output of $Q$.

resource

Background

Let’s fully understand these key quantities: $Q$, $V$, and $A$.

For a stochastic policy $\pi$, $Q$ is the value of choosing the action $a$ at the state $s$.

$$Q^\pi(s,a) = \mathbf{E} [R_t | s_t = s, a_t = a, \pi ]$$

$V$ tells us how good it is to be in the state $s$.

$$V^\pi(s) = \mathbf{E} [Q^\pi(s,a)]$$

Expectation is the mean of a random variable. Take $V$ as the mean of the value of each action choice.

$A$ relates $V$ to $Q$, tells us how good an action is relative to other action choices.

$$Q^\pi(s,a) = V^\pi(s) + A^\pi(s, a)$$

Two Streams: Value and Advantage

Why separate $V$ and $A$ in the first place?

There’s a reason for this: in fact, sometimes a state’s value is irrelevant to the value of actions. It is especially true for the states where actions don’t make any relevant difference to the environment.

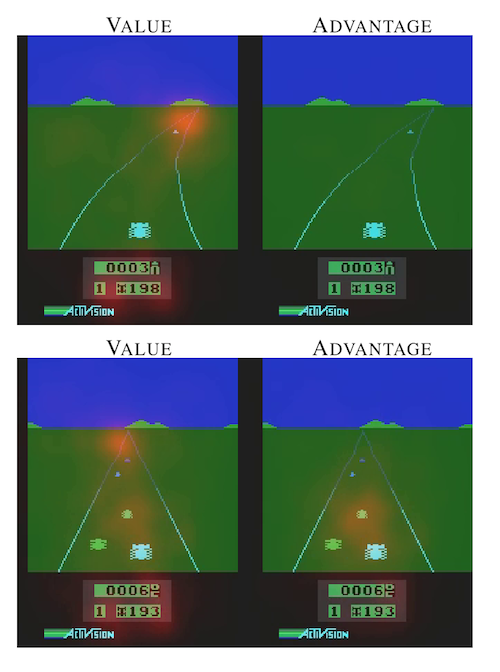
Take the Atari game Enduro for instance. Below is the saliency maps of two time steps. When cars are in front (bottom), the agent needs to move to the left or right to avoid collisions. The choice of action is very relevant. On the other hand, when no cars are in front (top), collisions are not our concern and the choice of action becomes irrelevant in this case.

resource

Note that value and advantage focus on different things. While the value function always pays attention to the score, the road, and the horizon where the new cars appear, the advantage function pays attention only when cars are in front and collisions are imminent.

The takeaway is value and advantage can be learned separately. It is possible to estimate a state’s value without estimating each action choice’s value. In other words, sometimes the same state value could be shared between multiple actions in that state, there are less to learn and therefore faster to converge.

Why then, produce Q as the output? You might ask. We want the dueling network to work out of the box with existing Q networks algorithms. For example, the convolution network in DQN outputs Q. With Q as the output, we could simply replace the convolution network in DQN with the dueling network and start training. This wouldn’t be possible if $V$ and $A$ are used as the output directly.

Zero Advantage

Aggregating $V$ and $A$ directly to get $Q$ would be naive.

$$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + A(s,a;\theta,\alpha)$$

Where $\theta$ is the parameters for the convolutional layers, $\alpha$ is the parameters for advantage, and $\beta$ is the parameters for value.

To learn an optimal policy, we will want to ensure a zero advantage for the chosen action. To understand this, let’s revisit the definition of advantage:

$$Q^\pi(s,a) = V^\pi(s) + A^\pi(s, a)$$

Note it implies $\mathbf{E} [A^\pi(s, a)] = 0$, because

$$\begin{split} V^\pi(s) &= \overbrace{\sum_a Q^\pi(s, a) p(a \vert s)}^{\mathbf{E} [Q^\pi(s,a)]} \\ &= \sum_a (\overbrace{V^\pi(s) + A^\pi(s, a)}^{Q^\pi(s, a)}) p(a \vert s) \\ &= V^\pi(s) + \underbrace{\sum_a A^\pi(s, a) p(a \vert s)}_{\mathbf{E} [A^\pi(s, a)] = 0} \end{split}$$

The same applies to a deterministic policy, where $a^* = {argmax}_{a’} {Q(s, a')}$ and $V(s) = Q(s,a^*)$, and thus $A(s,a^*) = 0$.

$Q$, $V$, and $A$ are all estimations, and estimations involve errors. During learning, the network propagates estimation errors backward to update the parameters accordingly. However, the issue of the naive approach is inidentifiability. We cannot recover $V$ and $A$ uniquely from a given $Q$. For example, the value 10 can be the sum of 4 plus 6, or 3 plus 7, or 5 plus 5, and so on. The network could allocate any amount of error to each stream during backpropagation, making no guarantee of a zero advantage and therefore learning a bad policy.

We could instead add an additional term to ensure a zero advantage.

$$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + (\underbrace{A(s,a;\theta,\alpha) - \max_{a' \in \vert \mathcal{A} \vert} A(s,a’;\theta,\alpha)}_\text{This term is 0 for a*})$$

For the chosen action $a^*$, $A(s,a^*;\theta,\alpha) = \max_{a' \in \vert \mathcal{A} \vert} A(s,a’;\theta,\alpha)$, making $A(s,a^*;\theta,\alpha) - \max_{a' \in \vert \mathcal{A} \vert} A(s,a’;\theta,\alpha) = 0$, and we obtain $Q(s, a^*;\theta,\alpha,\beta) = V(s;\theta,\beta)$.

The additional term acts as a target guiding the network to learn $A$. However, this target is always changing: following the target, the network updates its parameters, the updated network selects the next sample, then the selected sample updates the target. This is the known moving target issue for DQN.

Mean is more stable than max. Replacing the max operator with average could help to stabilize the learning:

$$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + (A(s,a;\theta,\alpha) - \frac{1}{|A|} \sum_{a'} {A(s,a’;\theta,\alpha)})$$

References

[1] Wang, Z., Schaul, T., Hessel, M., van Hasselt, H., Lanctot, M., & de Freitas, N. (2015). Dueling Network Architectures for Deep Reinforcement Learning.